Desvelando la fórmula de la probabilidad: El Teorema de Moivre en detalle
En el mundo de las matemáticas, la probabilidad es una herramienta fundamental para comprender y predecir eventos inciertos. Uno de los teoremas más importantes en este campo es el Teorema de Moivre, el cual nos permite calcular la probabilidad de que ocurra un evento específico en una distribución binomial.
El Teorema de Moivre es una extensión del Teorema del Límite Central, el cual establece que la suma de un gran número de variables aleatorias independientes y con la misma distribución tiende a seguir una distribución normal. Este teorema es esencial para el estudio de la probabilidad y ha sido utilizado en diversos campos como la estadística, la física y la economía.
En este artículo, exploraremos en detalle el Teorema de Moivre y su importancia en el cálculo de probabilidades. Descubriremos cómo se aplica este teorema en situaciones reales y cómo podemos utilizarlo para tomar decisiones informadas basadas en datos probabilísticos. ¡Prepárate para desvelar la fórmula de la probabilidad!
Teorema de Existencia
El Teorema de Existencia es uno de los pilares fundamentales del Teorema de Moivre. Este teorema establece que, para cualquier número real x y cualquier número entero n, existe un número complejo z tal que:
x = cos(z)
Este teorema es esencial para comprender la fórmula de la probabilidad y su relación con el Teorema de Moivre. Nos permite establecer una conexión entre los números reales y los números complejos, lo cual es fundamental para el estudio de la probabilidad.
Introducción al Teorema de Moivre
El Teorema de Moivre es una herramienta fundamental en el campo de la probabilidad y la estadística. Fue desarrollado por el matemático francés Abraham de Moivre en el siglo XVIII y ha sido utilizado ampliamente desde entonces.
Este teorema establece una relación entre la probabilidad de que ocurra un evento y la distribución normal estándar. En otras palabras, nos permite calcular la probabilidad de que un evento suceda dentro de un rango específico.
El Teorema de Moivre es especialmente útil cuando se trabaja con variables aleatorias binomiales, es decir, cuando se tienen dos posibles resultados para cada experimento. Nos permite aproximar la distribución binomial a una distribución normal, lo que simplifica los cálculos y facilita el análisis de los datos.
La fórmula del Teorema de Moivre
La fórmula del Teorema de Moivre se expresa de la siguiente manera:
P(x) = (1/√(2πnq)) * e^(-((x-np)^2)/(2npq))
Donde:
- P(x) es la probabilidad de que ocurra el evento x.
- n es el número de experimentos.
- p es la probabilidad de éxito en cada experimento.
- q es la probabilidad de fracaso en cada experimento (q = 1 – p).
- x es el número de éxitos que se desea calcular.
- e es la base del logaritmo natural (aproximadamente 2.71828).
- π es el valor de pi (aproximadamente 3.14159).
Esta fórmula nos permite calcular la probabilidad de que ocurra un número específico de
Historia del Teorema de Moivre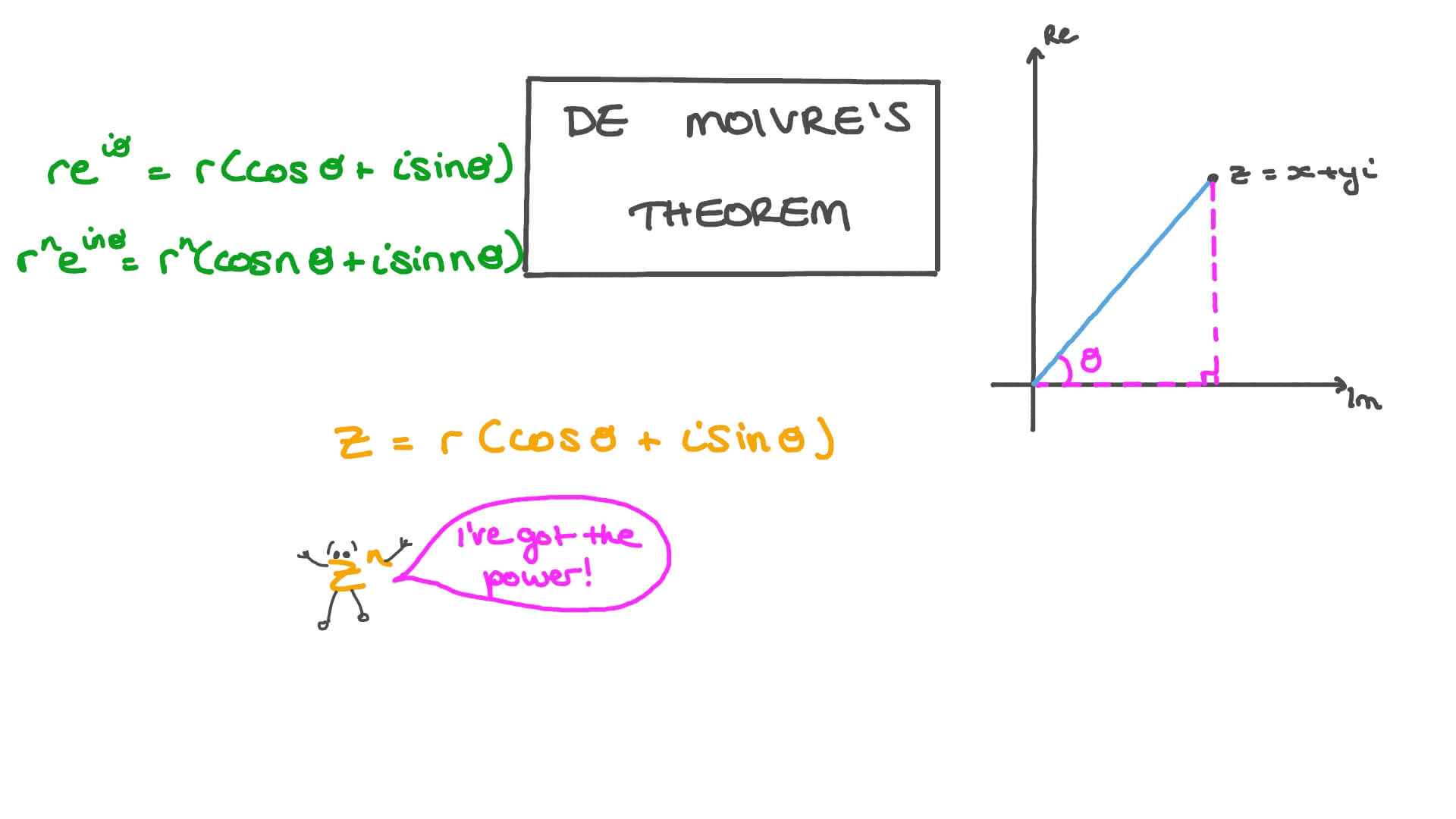
El Teorema de Moivre es una fórmula matemática que se utiliza para calcular la probabilidad de eventos en situaciones de incertidumbre. Fue desarrollado por el matemático francés Abraham de Moivre en el siglo XVIII.
Moivre fue uno de los pioneros en el campo de la teoría de la probabilidad y su trabajo sentó las bases para el desarrollo de esta disciplina. Su teorema establece que la probabilidad de que ocurra un evento en un número determinado de intentos es igual a la suma de las probabilidades de que ocurra un número específico de veces.
El Teorema de Moivre ha sido ampliamente utilizado en diversos campos, como la estadística, la física y la economía. Su importancia radica en que proporciona una herramienta matemática para calcular la probabilidad de eventos en situaciones de incertidumbre, lo que permite tomar decisiones informadas y realizar predicciones basadas en datos.
Aplicaciones del Teorema de Moivre
El Teorema de Moivre es una herramienta fundamental en el campo de la probabilidad y tiene diversas aplicaciones en diferentes áreas. Una de las aplicaciones más comunes es en el cálculo de probabilidades en experimentos repetidos. Por ejemplo, si queremos saber la probabilidad de obtener un número específico al lanzar un dado varias veces, podemos utilizar el Teorema de Moivre para calcular esta probabilidad.
Otra aplicación importante del Teorema de Moivre es en el campo de la estadística. Este teorema nos permite calcular la probabilidad de obtener un cierto número de éxitos en un número determinado de ensayos independientes. Por ejemplo, si queremos saber la probabilidad de obtener exactamente 3 caras al lanzar una moneda 10 veces, podemos utilizar el Teorema de Moivre para calcular esta probabilidad.
Además, el Teorema de Moivre también se utiliza en el campo de la teoría de juegos. En juegos de azar como el póker o la ruleta, este teorema nos permite calcular la probabilidad de obtener ciertas combinaciones de cartas o números. Esto es especialmente útil para los jugadores que desean tomar decisiones informadas basadas en la probabilidad de obtener ciertos resultados.
En resumen, el Teorema de Moivre tiene una amplia gama de aplicaciones en el campo de la probabilidad, la estadística y la teoría de juegos. Su uso nos permite calcular la probabilidad de obtener ciertos resultados en experimentos repetidos, en eventos aleatorios y en juegos de azar. Es una herramienta fundamental para aquellos que desean comprender y utilizar la probabilidad en diferentes contextos.
Explicación matemática del Teorema de Moivre
El Teorema de Moivre es una herramienta fundamental en el campo de la probabilidad y la estadística. Este teorema establece una relación entre las potencias de un número complejo y las funciones trigonométricas. Su formulación matemática es la siguiente:
Para cualquier número complejo z y cualquier número entero n, se cumple la siguiente igualdad:
(cos θ + i sen θ)^n = cos(nθ) + i sen(nθ)
Donde θ es el ángulo en radianes y i es la unidad imaginaria.
Este teorema es especialmente útil para calcular las probabilidades de eventos en experimentos repetidos. Por ejemplo, si queremos saber la probabilidad de obtener un número par al lanzar un dado n veces, podemos utilizar el Teorema de Moivre para simplificar los cálculos.
En resumen, el Teorema de Moivre nos permite relacionar las potencias de un número complejo con las funciones trigonométricas, lo cual resulta de gran utilidad en el campo de la probabilidad y la estadística.
Prueba del Teorema de Moivre
El Teorema de Moivre es una herramienta fundamental en el campo de la probabilidad y la estadística. Este teorema establece una relación entre la probabilidad de que ocurra un evento y la distribución normal estándar. Para entender cómo funciona este teorema, es necesario realizar una prueba que demuestre su validez.
La prueba del Teorema de Moivre se basa en el uso de la distribución binomial y la aproximación de la distribución normal. La distribución binomial se utiliza para calcular la probabilidad de que ocurra un evento en un número determinado de ensayos independientes. Por otro lado, la distribución normal es una distribución continua que se utiliza para modelar fenómenos naturales.
Para realizar la prueba del Teorema de Moivre, se parte de una distribución binomial con un número grande de ensayos y una probabilidad de éxito constante. A medida que el número de ensayos aumenta, la distribución binomial se aproxima cada vez más a una distribución normal. Esto se debe a la Ley de los Grandes Números, que establece que a medida que se realizan más ensayos, la media de los resultados se acerca a la media teórica.
Relación del Teorema de Moivre con la distribución normal
El Teorema de Moivre es una herramienta fundamental en el campo de la probabilidad y estadística. Este teorema establece una relación entre la distribución binomial y la distribución normal, lo que permite aproximar los resultados de una distribución binomial a través de la distribución normal.
La distribución binomial es utilizada para modelar experimentos que tienen dos posibles resultados, como por ejemplo lanzar una moneda al aire y obtener cara o cruz. Por otro lado, la distribución normal es una distribución continua que se utiliza para modelar fenómenos naturales y sociales.
El Teorema de Moivre establece que cuando el número de ensayos de una distribución binomial es grande y la probabilidad de éxito es moderada, la distribución binomial se puede aproximar a una distribución normal. Esto significa que podemos utilizar la distribución normal para calcular probabilidades en experimentos que involucran un gran número de ensayos.
Teorema de Moivre y la teoría de límites
El Teorema de Moivre es un resultado fundamental en la teoría de probabilidades que establece una relación entre la probabilidad y la teoría de límites. Este teorema, formulado por el matemático Abraham de Moivre en el siglo XVIII, es ampliamente utilizado en el campo de la estadística y la probabilidad.
El Teorema de Moivre establece que la distribución de probabilidad de la suma de n variables aleatorias independientes y idénticamente distribuidas se aproxima a una distribución normal cuando n tiende a infinito. En otras palabras, si tenemos una muestra grande de variables aleatorias, la distribución de la suma de estas variables se asemejará a una distribución normal.
Este resultado es de gran importancia en la teoría de probabilidades, ya que permite simplificar el cálculo de probabilidades en situaciones donde se tienen muchas variables aleatorias. Además, el Teorema de Moivre proporciona una base teórica para la utilización de la distribución normal en la aproximación de probabilidades en diversos problemas prácticos.
Teorema de Moivre y la teoría de la probabilidad
El Teorema de Moivre es una herramienta fundamental en la teoría de la probabilidad. Este teorema establece una relación entre la probabilidad de un evento y el número de veces que dicho evento ocurre en un experimento repetido un gran número de veces. En otras palabras, nos permite calcular la probabilidad de obtener un cierto número de éxitos en una serie de ensayos independientes.
El teorema establece que si tenemos un experimento con dos posibles resultados, éxito o fracaso, y la probabilidad de éxito en cada ensayo es constante, entonces la distribución de probabilidad de obtener un número específico de éxitos sigue una distribución normal. Esto significa que podemos utilizar la fórmula de la distribución normal para calcular la probabilidad de obtener un cierto número de éxitos en una serie de ensayos.
El Teorema de Moivre es especialmente útil cuando trabajamos con grandes muestras o cuando queremos aproximar la distribución binomial a una distribución normal. Esto nos permite simplificar los cálculos y obtener resultados más precisos. Además, el teorema también nos permite calcular la probabilidad acumulada, es decir, la probabilidad de obtener un número igual o menor de éxitos en una serie de ensayos.
Teorema de Moivre y la estadística
El Teorema de Moivre es una herramienta fundamental en el campo de la estadística que permite calcular la probabilidad de ocurrencia de eventos en un experimento aleatorio. Este teorema establece una relación entre la distribución binomial y la distribución normal, lo que lo convierte en una herramienta poderosa para el análisis de datos.
La distribución binomial se utiliza para modelar experimentos en los que se realizan una serie de ensayos independientes, cada uno con dos posibles resultados: éxito o fracaso. Por otro lado, la distribución normal es una distribución continua que se utiliza para modelar fenómenos naturales y sociales que tienden a agruparse alrededor de un valor central.
El Teorema de Moivre establece que, cuando el número de ensayos en un experimento binomial es grande y la probabilidad de éxito es moderada, la distribución binomial se aproxima a una distribución normal. Esto significa que podemos utilizar la distribución normal para calcular la probabilidad de ocurrencia de eventos en un experimento binomial, lo que simplifica enormemente los cálculos.
Teorema de Moivre y la teoría de los números
El Teorema de Moivre es una herramienta fundamental en la teoría de la probabilidad y los números complejos. Este teorema establece una relación entre las potencias de un número complejo y las funciones trigonométricas. Fue formulado por el matemático francés Abraham de Moivre en el siglo XVIII y ha sido utilizado ampliamente en diversos campos de las matemáticas y la física.
El teorema establece que si z es un número complejo de la forma z = r(cosθ + isenθ), donde r es el módulo de z y θ es el argumento de z, entonces la potencia n-ésima de z se puede expresar como:
z^n = r^n(cos(nθ) + isen(nθ))
Este resultado es de gran importancia en la teoría de la probabilidad, ya que permite calcular la probabilidad de eventos en experimentos repetidos. Además, el Teorema de Moivre también tiene aplicaciones en la teoría de números, especialmente en la teoría de congruencias y en la resolución de ecuaciones polinómicas.
Teorema de Moivre y la teoría de la información
El Teorema de Moivre es una herramienta fundamental en la teoría de la probabilidad y la estadística. Este teorema establece una relación entre la distribución normal y la distribución binomial, lo que permite calcular probabilidades de eventos en situaciones donde se cumplen ciertas condiciones.
En la teoría de la información, el Teorema de Moivre es utilizado para modelar y analizar la transmisión de datos en sistemas de comunicación. Este teorema permite calcular la probabilidad de que un mensaje sea transmitido correctamente a través de un canal de comunicación, teniendo en cuenta el ruido y las posibles interferencias.
El Teorema de Moivre es una herramienta poderosa que ha sido utilizada en diversos campos, desde la física y la ingeniería hasta la economía y la biología. Su aplicación en la teoría de la información ha permitido el desarrollo de sistemas de comunicación más eficientes y confiables.

